|
|
|
Abstract
Do governments satisfy an intertemporal budget constraint? This paper uses a panel of U.S. state data from 1978-1998 to empirically investigate whether primary surpluses respond to rising debt/GDP ratios. Instead of relying solely on the time-series characteristics of various data series, the paper focuses on the response of primary surpluses when cyclical fluctuations in output and government spending are explicitly considered. Results suggest no surplus response to the accumulation of debt, whether or not cyclical fluctuations are controlled for, in contrast to similar studies done using U.S. federal government data.
Keywords: fiscal policy; fiscal sustainability; public debt; budget deficits
JEL: E62, H63, H74
1 Introduction
Do governments implement sustainable fiscal policies? That is, do they pursue fiscal policies that will result in “manageable” deficit and debt levels rather than explosive debt and insolvency? This is an important question for several reasons. Clearly, governments lose a stabilization tool if the use of the public budget, due to insolvency, is no longer an option during economic downturns. Aging populations that will increase future liabilities require “appropriate” levels of debt today. Large debt burdens may hamper the central bank’s ability to resist the temptation to inflate the debt away. The debt crisis in Greece and multiple countries’ repeated violations of the Eurozone’s debt and deficit limits have renewed interest in the issue of fiscal sustainability.
Given its importance, there is surprisingly no universally agreed upon definition for the sustainability of fiscal policy (see Balassone and Franco (  2000 2000) for a discussion of various interpretations). Most empirical papers focus on the government’s intertemporal budget constraint: the current value of the public debt must equal the discounted value of future primary (non-interest) surpluses. A violation of the intertemporal budget constraint means that debt will grow at a rate faster than the growth rate of the economy. If the government were able to borrow to pay interest costs, it would face no constraint and would be engaging in a Ponzi scheme.
One stream in the empirical literature on debt sustainability focuses on testing relevant variables for stationarity or co-integration to determine if the government intertemporally balances its budget (see, e.g. Hamilton and Flavin,  1986 1986; Trehan and Walsh,  1988 1988,  1991 1991; Bohn,  1991 1991; Kremers,  1989 1989; Hakkio and Rush,  1991 1991; and Quintos,  1995 1995). However, Bohn (  2007 2007) has faulted these types of tests as invalid, given that the intertemporal budget constraint is satisfied if either the debt or revenue and with-interest spending series are integrated of arbitrarily higher order, i.e. if they are stationary after an arbitrary sequence of differencing.
Additionally, these types of tests have been criticized in a series of papers by Bohn (  1995 1995,  1998 1998,  2008 2008) as uninformative because in the case of uncertainty, finding an appropriate rate at which to discount future surpluses is problematic. In particular, Bohn (  1995 1995) shows that bond returns are unsuitable as discount rates in transversality conditions as the relevant uncertainty pertains to the level of future total public debt, and not the riskiness of specific debt securities. Thus studies focusing on unit root and cointegration tests – that is, testing whether various fiscal time series are consistent with the hypothesis that the expected present value of primary balances equals discounted initial debt – are incorrect as they use the wrong discount rate.
Given these problematic issues with time series tests in this context, Bohn (  1998 1998) focuses on testing a fiscal policy reaction function. Using Barro’s (  1979 1979) tax smoothing model and Barro’s (  1986 1986) and Sahasakul’s (  1986 1986) empirical work as starting points, Bohn (  1998 1998) shows that if the primary (noninterest) budget surplus-income ratio responds positively to changes in the debt-income ratio, then fiscal policy is sustainable. He also shows that this relationship can be obscured by war-time spending and cyclical fluctuations in output, thus providing an additional explanation as to why unit root tests might fail to find evidence of corrective action. Importantly, this method is also independent of the discount rate used. This theoretical and empirical strategy has been termed the “fiscal reaction function” approach or “model based sustainability” approach. Using U.S. federal government data, Bohn (  1998 1998) finds that the primary surplus-income is an increasing function of the debt-GDP ratio; that is, the intertemporal budget constraint is satisfied for the U.S.
Several papers have used the fiscal reaction function approach of Bohn (  1998 1998) to test for sustainability in other countries. Greiner, Köller and Semmler (  2007 2007) focus on Italy (for its high debt/GDP ratio) and France, Germany, and Portugal (violators of the Maastricht treaty’s deficit limit of three percent of GDP) and find evidence for sustainability. Mendoza and Ostry (  2008 2008) use panels of advanced and emerging countries and also find that fiscal policy is responsible – the primary fiscal balance responds positively to changes in debt.
This paper uses techniques similar to those of Barro (  1986 1986) and Bohn (  1998 1998) and investigates the response of U.S. states’ primary surplus-income ratios to their debt-income ratios, in order to shed some light on the sustainability of fiscal policies among members of a monetary union. As in Barro (  1986 1986) and Bohn (  1998 1998), cyclical variables are constructed and controlled for in a consideration of the surplus response to debt. Also as in Barro (  1986 1986) and Bohn (  1998 1998), the paper considers how this relationship is affected if an interest rate variable is included. Findings are robust and indicate that U.S. states’ primary surplus-income ratios do not respond to their debt-income ratios, in contrast to Bohn’s (  1998 1998) results for the federal government. This result also runs counter to Mendoza and Ostry (  2008 2008) and Greiner and Semmler (  2007 2007). However, Greiner and Semmler (  2007 2007) focuses on individual countries and the samples in Mendoza and Ostry (  2008 2008) mix Eurozone and non-Eurozone countries. It is also found that states do not respond to credit market pressure, in the sense that the primary budget surplus-income ratio does not increase in response to an increasing risk premium.
2 The use of state data
The existence of various types of balanced budget rules and tax and expenditure limitations in U.S. states would seem to hinder their ability to run deficits/surpluses and thus limit the application of an intertemporal, optimizing model. However, while Bohn and Inman ( 1996) find that states that have regulations limiting the amount of debt have lower average deficits, Sørensen, Wu and Yosha ( 1996) find that states that have regulations limiting the amount of debt have lower average deficits, Sørensen, Wu and Yosha ( 2001) find that states are able to systematically smooth income shocks, suggesting that in practice states are not bound by these requirements. Kula ( 2001) find that states are able to systematically smooth income shocks, suggesting that in practice states are not bound by these requirements. Kula ( 2014 ) examines the extent of public consumption smoothing at the state and local level. Furthermore, Chaney, Copley and Stone ( 2014 ) examines the extent of public consumption smoothing at the state and local level. Furthermore, Chaney, Copley and Stone ( 2002) find that budget stressed states underfund their pensions and choose discount rates that obscure the underfunding in order to meet balanced budget requirements. Anecdotal evidence of budgetary “finesse” can be found in newspapers on a regular basis, e.g.: “N.J. Pension Fund Endangered by Diverted Billions” (The New York Times 4/4/07); “The Illusion of Pension Savings” (The New York Times 9/17/10). For more examples of state and local governments skirting balanced budget laws/budget regulations, see, Holtz-Eakin, Rosen and Tilly ( 2002) find that budget stressed states underfund their pensions and choose discount rates that obscure the underfunding in order to meet balanced budget requirements. Anecdotal evidence of budgetary “finesse” can be found in newspapers on a regular basis, e.g.: “N.J. Pension Fund Endangered by Diverted Billions” (The New York Times 4/4/07); “The Illusion of Pension Savings” (The New York Times 9/17/10). For more examples of state and local governments skirting balanced budget laws/budget regulations, see, Holtz-Eakin, Rosen and Tilly ( 1994). 1994).
3 Model and estimating equations
This section reviews work by Barro ( 1979, 1979,  1986, 1986,  1989) and Sahasakul ( 1989) and Sahasakul ( 1986) that is used by Bohn ( 1986) that is used by Bohn ( 1998) to develop a fiscal policy reaction function estimating equation. 1998) to develop a fiscal policy reaction function estimating equation.
According to Barro’s (  1979 1979) tax smoothing model, an optimizing government smoothes the costs of distortionary taxation over time by adjusting its tax rate only in response to changes in permanent government spending or its debt level. Temporary changes in spending or income result in budget deficits or surpluses. Denote the real cost of collecting taxes at time t by Zt. This cost is a time invariant, linearly homogeneous function of real tax revenue Tt and real aggregate output Yt. Denote the tax rate by τt. Thus Zt = F( Tt , Yt) = f ( τt) Yt where f ' > 0, f '' > 0.
The government chooses its sequence of tax rates to minimize this convex excess burden function subject to two constraints: raised tax revenue must equal exogenously given government spending (Gt), and the government cannot engage in perpetual debt finance (where B0 is initial debt):
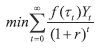 |
|
subject to and The solution to this optimization problem is for the government to set a constant tax rate: τt+s = τt ∀s ≥ 0. Re-writing the government’s budget constraint beginning at time i gives
Imposing the tax smoothing condition of τt = τi for all t > 1 on the budget constraint gives the tax rate at time i as 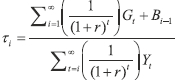 | (1) |
Assume that in steady state Gt and Yt grow at rate n. Then “normal” or permanent (the annuity value of current and expected expenditures) spending Gi* and “normal” or permanent output (constant for t ≥ 1) sequences can be defined as those that satisfy
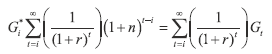 |
|
and
Then, as in Barro (  1986 1986,  1989 1989), substituting the permanent variables into equation (1) leads to period i tax rate 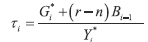 | (2 ) ) |
The period i budget surplus is given by the government’s budget constraint:
| Gi + rBi-1 – τiYi = Bi – Bi-1 | (3 ) ) |
Substituting equation (2) into equation (3) and re-arranging terms gives: | Bi – Bi-1 = Gi – Gi* + [(Yi* – Yi) ⁄ (Yi*] [Gi* + (r – n)Bi-1] + nBi-1 |
|
or | Bi – Bi-1 = Gi – Gi* + (1 – Yi ⁄ Yi*)[Gi* + (r – n)Bi-1] + nBi-1 | (4 ) ) |
where ( r – n) Bi–1 is assumed to be small relative to Gi*, Gi – Gi* is temporary spending, or GVAR; and (1 – Yi /Yi*) Gi* is cyclical output, or YVAR. Thus the surplus responds to increases in temporary spending and cyclical output shortfalls, as well as debt level.
Bohn (  1998 1998) uses the above derivation to motivate his estimating equation (from equation (4)): | st = α0 + β1dt + β2GVARt + β3YVARt + εt | (5 ) ) |
where st is the primary surplus divided by output (GNP is used as his sample begins in 1916); dt is the outstanding debt at the beginning of period t divided by GNP; GVARt is the temporary government spending to output ratio; and YVARt is a measure of the cyclical fluctuation of output. Using a sample from 1916-1995, he finds that the primary surplus is an increasing function of the debt-GNP ratio, meaning that the U.S. government systematically responds to changes in the debt-GNP ratio and behaves according to an intertemporal budget constraint, with this result being sensitive to the inclusion of temporary spending and output. When these variables are left out, the relationship disappears. In one criticism of statistically based studies, Bohn (  1998 1998) notes that regressions testing for a unit root in the debt/GDP ratio are misspecified because of the omission of the cyclical variables GVAR and YVAR – and therefore it is not surprising that they cannot reject the unit root.
As an extension, consider a non-constant interest rate, as discussed in Barro (  1989 1989). If the interest rate varies around a trend, the permanent interest rate (i.e. an asset paying r*i–1 has the same present value of an asset with varying payments) is given by and equation (4) becomes | Bi – Bi-1 = Gi – Gi* + (1 – Yi ⁄ Yi*)[Gi* + (ri-1 – n)Bi-1] + nBi-1 + (ri-1 – ri-1*)Bi-1 | (6 ) ) |
where ( ri-1 – r*i-1) Bi-1 represents “temporary interest payments” ( RVAR). Thus the surplus also responds to movements in interest rates around trend levels.
Equation (6) can be written as | st = GVARt + YVARt + dt + RVARt + εt | (7 ) ) |
Bohn (  1998 1998) also examines whether the debt-surplus relationship for the U.S. is invariant to the real interest rate by estimating equation (7). He finds that the positive relationship between debt and surplus is not affected by various real interest rate measures, such as the average real return on government debt.
This paper uses a panel of U.S. states and unique data on interest rates to examine fiscal sustainability. Specifications with and without the cyclical variables will be used to compare results to Bohn’s (  1998 1998) finding that their inclusion affects the impact of debt on the surplus when federal data is used. Additionally, specifications with and without an interest rate variable will be used to check Bohn’s (  1998 1998) finding that its inclusion does not affect the impact of debt on the surplus. Importantly, this specification also sheds light on whether or not the surplus responds to the interest rate; that is, whether credit markets influence government spending and taxing decisions.
For the panel, we have estimating equations: | sjt = α0 + β1djt + εjt | (8 ) ) |
| sjt = α0 + β1djt + β2GVARjt + β3YVARjt + εjt | (9 ) ) |
| sjt = α0 + β1djt + β2Rjt + εjt | (10 ) ) |
and | sjt = α0 + β1djt + β2Rjt + β3GVARjt + β4YVARjt + εjt | (11 ) ) |
where Sjt is the primary (noninterest) budget surplus-income ratio for state j at time t, djt is the beginning of period t debt-income ratio, Rjt is the period t interest rate, GVARjt is cyclical government spending, and YVARjt is cyclical output. A positive coefficient on djt would indicate that the government takes corrective action. Additionally, a positive coefficient on the interest rate variable would indicate that the government takes corrective action in response to higher borrowing costs. Note, however, the potentially endogenous relationship between the interest rate and the surplus. A larger primary surplus, e.g. may indicate a lower likelihood of default, and thus correspond to a lower interest rate. Given the potential endogeneity between the surplus and the interest rate, the lagged interest rate is used. Additionally, to capture unobserved, time invariant state-specific attributes that may affect spending, state fixed effects are included in the estimation. With the panel data approach and the use of a state fixed effects parameter to capture state-specific time invariant characteristics, some inherent differences across states that account for differences in the interest rates are accounted for in the specification, and are thus less likely to be caught in the residual, allowing for the lagged interest rate to be an acceptable method to control for endogeneity.
The final estimation issue concerns spurious correlation. Augmented Dickey Fuller tests on each data series were unable to reject that they were unit root processes. However, given the length of the series and the low power of ADF tests, this result is not unexpected. Each series with state and time fixed effects removed was plotted over time to determine whether the removal of time fixed effects would be sufficient for stationarity. The graphs for each of the series suggest that the removal of time fixed effects is, in fact, sufficient for stationarity. Estimating equations are thus: | sjt = αj + γt + β1djt + εjt | (12 ) ) |
| sjt = αj + γt + β1djt + β2GVARjt + β3YVARjt + εjt | (13 ) ) |
| sjt = αj + γt + β1djt+β2Rjt-1 + εjt | (14 ) ) |
and | sjt = αj + γt + β1djt + β2Rjt-1 + β3GVARjt + β4YVARjt + εjt | (15 ) ) |
3.1 Formation of the cyclical variables GVARjt and YVARjt
As in Barro ( 1986), Sahasakul ( 1986), Sahasakul ( 1986) and Bohn ( 1986) and Bohn ( 1998), the permanent and temporary series must be constructed; each of these uses methods from Barro ( 1998), the permanent and temporary series must be constructed; each of these uses methods from Barro ( 1979) and they begin by decomposing government spending into defense and nondefense components. The series for permanent defense spending is derived from the premise that actual defense spending is determined by lagged casualty rate measures and the lagged stock of military equipment. Temporary spending is actual spending minus permanent spending. For U.S. states, this method would not be appropriate. 1979) and they begin by decomposing government spending into defense and nondefense components. The series for permanent defense spending is derived from the premise that actual defense spending is determined by lagged casualty rate measures and the lagged stock of military equipment. Temporary spending is actual spending minus permanent spending. For U.S. states, this method would not be appropriate.
The temporary spending variable GVARjt is found for each state for each time period in two steps. First, the sensitivity of government expenditure to the unemployment rate and the growth rate of output and its lag is determined. The cyclical spending variable is then constructed by considering these sensitivity parameters and the deviations of the actual unemployment rate and the growth rate of output at time t (and its lag) from their “permanent”, or estimated weighted average levels at time t.
Specifically, consider the formation of the noncyclical unemployment rate and the growth rate of output. To construct these series, the underlying data generating process for each observed series must be determined. After the removal of time fixed effects, graphs of the unemployment rate and the growth rate of output indicate that an AR(1) process is a good descriptor for each. Focusing on the unemployment rate series, the data generating process for the unemployment rate with time fixed effects removed can be written as: | ujt = Γj + γ1ujt-1 + εujt | (16) |
| ujt+s = Γj + γ1ujt+s-1 + εujt+s | (17) |
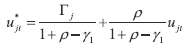 | (18) |
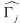 and and 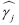 are found. They are used in equation (18) to obtain the complete series for the estimated weighted average unemployment rate. A similar procedure is used to find the series for the estimated weighted average of the growth rate of output. are found. They are used in equation (18) to obtain the complete series for the estimated weighted average unemployment rate. A similar procedure is used to find the series for the estimated weighted average of the growth rate of output.
The sensitivity of spending to the unemployment rate and the growth rate of output and its lag is found by estimating: 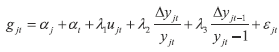 | (19 ) ) |
Estimated parameters 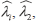 and 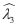 are used along with u*jt, the estimated weighted average unemployment rate series, and output growth rate series, 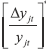 , to calculate GVARjt.
Temporary output YVARjt is formed in a manner similar to that of Barro ( 1986) and Bohn ( 1986) and Bohn ( 1998). Barro ( 1998). Barro ( 1986) discusses the difficulties in forming a permanent, and therefore temporary, output series, and shows the algebraic manipulation necessary to arrive at a convenient form for temporary output: 1986) discusses the difficulties in forming a permanent, and therefore temporary, output series, and shows the algebraic manipulation necessary to arrive at a convenient form for temporary output:
where 5.4% is the assumed natural unemployment rate and g* is the permanent government spending to output ratio. Barro (  1986 1986) also discusses why the above measure is preferred to various alternatives attempted. | YVARjt = (ujt - u.t) g*jt |
|
| YVARjt = (ujt - u.t) g*jt |
|
4 Data
The primary (noninterest) surplus-income ratio, sjt is defined as state and local direct general expenditure minus interest payments on general debt minus tax revenue divided by gross state product (GSP). The combined state and local sector is used to avoid problems resulting from the differing assignment of functional responsibilities of state and local governments across states. The debt-income ratio, djt , is long term debt as a percentage of GSP. Data on direct general expenditure, interest payments on general debt, long term debt and total revenue are from Government Finances, Bureau of the Census, for the years 1978-1998. GSP is from the Census Bureau; the unemployment rate series are from the Bureau of Labor Statistics (1978-1998). The sample covers the years 1978-1998, except for GSP, where data from 1963-2009 are used to estimate the parameters used in constructing the noncyclical series.
Regressions which include the interest rate raise an issue regarding the appropriate variable to use. As discussed in Bohn (2005), past statistical based studies have confused the uncertainty about the level of future total public debt, which is what is needed, with the riskiness of specific debt securities, which is what researchers have used. This paper uses a unique data source to solve this problem. The Chubb Relative Value Study was started in 1973 (ending in 1998) by the Chubb Insurance Company to address the lack of information available on municipal bond trading values, as the market for state general obligation bonds is typically very thin, resulting in a lack of availability of market prices for individual issues (Bayoumi, Goldsteina and Woglom,  1995 1995; Park,  1997 1997; Liu and Thakor,  1984 1984). Additionally, state general obligation bond issues may vary for several reasons, including call provisions, maturity dates, tax issues, and insurance coverage. Semi-annually, twenty to twenty-five sell-side traders at major brokerage firms dealing in tax exempt bonds were polled as to where they thought twenty-year comparable state general obligation bonds should trade relative to the chosen benchmark state, New Jersey (chosen as at the time it was close to the midpoint of state trading values and was seen as being stable regarding creditworthiness). The traders considered similar bonds for the states, so the difference in spreads reflects only differences in default risk, thus solving the problems of comparing state general obligation bond issues and isolating a default risk premium for each state. Importantly for the current paper, the default risk would clearly be tied to expectations of the future path of total public debt (and specifically not tied to the riskiness of a particular security), so using this measure avoids Bohn’s (2005) criticism of empirical work using the wrong interest rate when testing sustainability. Because the Chubb dana spans the period 1973-1998 and long term debt is available beginning in 1978, the sample data used runs from 1978 to 1998.
Given the uniqueness of the Chubb data in allowing for the comparison of state bond yields, they have been used in several papers including Goldstein and Woglom (  1992 1992) and Bayoumi, Goldstein, and Woglom (  1995 1995) in their investigation of the effect of rising government debt on state bond yields; Poterba and Rueben (  1999 1999,  2001 2001) which focus on the relationship between fiscal institutions and bond yields; and Andersen et al. (  2014 2014), which examines how the quality of fiscal governance, proxied for by the government’s ability to submit an on-time budget, affects state borrowing costs.
The survey excluded states that had no outstanding debt when the survey began (Arizona, Arkansas, Colorado, Idaho, Iowa, Indiana, Kansas, Nebraska, South Dakota, and Wyoming). Here, Puerto Rico (not a state), Alaska (unique in its relative oil and mineral endowments), and Hawaii (unique in its constitutional structure) are also excluded from the panel, leaving a full sample of thirty-eight states. The average Chubb yield for each state over the sample period 1973-1998 and other descriptive statistics are given in table 1.
Table 1Descriptive statistics DISPLAY Table
The average Chubb yield for each year for the sample period and the high-low spread are given in table 2. The recession years of 1976, 1982, and 1983 show the largest spreads while the smallest occur in 1998, a period of low inflation and unemployment and high growth for the U.S.
Table 2Average Chubb yields over all states and high-low spread by year DISPLAY Table
5 Results
Consider equations (12) and (13). If governments satisfy an intertemporal budget constraint in that they take corrective action in response to an increasing debtincome ratio, β1 is expected to be positive in equation (12). If this relationship is obscured by cyclical spending and output, we should find β1 to be positive in equation (13). The coefficients on cyclical spending and output should be negative. The same holds true for equations (14) and (15), which add the interest rate to the regressions; here, it should also be found that β2 is positive in equations (14) and (15).
First consider the results when the interest rate variable is not included. Table 3 contains results for pooled data; table 4 contains results when only state fixed effects are included; and table 5 contains results when both state and time fixed effects are included. The (a) section of each table does not include the cyclical variables; the (b) section does. Whether or not cyclical variables are included, the coefficient on the debt-income ratio is negative, contrary to theory, and statistically significant for all specifications (pooled, state fixed effects only included; state and time fixed effects included). The coefficients on cyclical spending and output are either statistically insignificant or are statistically significant and positive, contrary to what is predicted, except for the pooled regression, where the cyclical spending coefficient is negative and statistically significant at the ten percent level.
Table 3Asjt = α + β1djt + εjt DISPLAY Table Table 3Bsjt = α + β1djt + β2GVARjt + β3YVARjt + εjt DISPLAY Table Table 4Asjt = αj + β1djt + εjt DISPLAY Table Table 4Bsjt = αj + β1djt + β2GVARjt + β3YVARjt + εj DISPLAY Table Table 5Asjt = αj + Yt + β1djt + εjt DISPLAY Table Table 5Bsjt = αj + γt + β1djt + β2GVARjt + β3YVARjt + εjt DISPLAY Table
Tables 6-8 contain results for all of the above regressions, this time with the interest rate variable included. Table 6 contains results for pooled data; table 7 contains results when only state fixed effects are included; and table 8 contains results when both state and time fixed effects are included. The (a) section of each table does not include the cyclical variables; the (b) section does. As in all regressions which did not include the interest rate variable, whether or not cyclical variables are included, the coefficient on the debt-income ratio is negative and statistically significant for all specifications (pooled, state fixed effects only included; state and time fixed effects included). The coefficients on cyclical spending and output are either statistically insignificant or are statistically significant and positive, contrary to what is predicted, except for the pooled regression, where the cyclical output coefficient is negative and statistically significant at the ten percent level. Additionally, the coefficient on the interest rate risk premium is also negative and statistically significant whether or not cyclical variables are included, and for all specifications (pooled, state fixed effects only included; state and time fixed effects included). This suggests there is no response by governments in their spending and taxing behavior to credit market signals. The positive coefficient on the output gap when state and time fixed effects are included can be interpreted as states running a countercyclical fiscal policy or may reflect the greater responsiveness of tax revenues to downturns than government spending at the state level.
Table 6Asjt = α + β1djt + β2Rjt-1 + εjt DISPLAY Table Table 6Bsjt = α + β1djt + β2Rjt–1 + β3GVARjt + β4YVARjt + εjt DISPLAY Table Table 7Asjt = αj + β1djt + β2Rjt–1 + εjt DISPLAY Table Table 7Bsjt = αj + β1djt + β2Rjt–1 + β3GVARjt + β4YVARjt + εjt DISPLAY Table Table 8Asjt = αj + γt + β1djt + β2Rjt–1 + εjt DISPLAY Table Table 8Bsjt = αj + γt + β1djt + β2Rjt–1 + β3GVARjt + β4YVARjt + εjt DISPLAY Table
As a further check, adding the lagged surplus-income ratio as an independent variable to equation (15) and using Arellano and Bond (  1991 1991) difference GMM estimation supports the conclusion on the surplus-debt relationship reached above: the coefficient on the debt-income ratio is negative and statistically significant, while that for the interest rate is statistically insignificant from zero (one step estimates with robust test statistics) for various lag lengths used for instruments.
Finally, the sample is split into two groups based on a ranking by debt/GSP. The high debt states are those with debt at or above the mean of 14% of GSP (25 states); the low debt states have debt below 14% of GSP (13 states). Results are in table 9 (high debt) and 10 (low debt). (Results in tables 9 and 10 are robust to moving the four states with 14% debt levels into the low debt group.) For the high debt subsample, all results match the full sample when the cyclical variables are included; when the cyclical variables are not included, the coefficient on the debtincome ratio is negative and statistically significant while the interest rate coefficient is not significant. All results for the low debt subsample are not statistically significant different than zero. The overall conclusion remains the same as that with the full sample: the surplus-income ratio does not respond to the debt-income ratio in the way predicted by fiscal sustainability; nor does it respond to credit market signals.
Table 9Asjt = αj + γt + β1djt + β2Rjt–1 + εjt DISPLAY Table Table 9Bsjt = αj + γt + β1djt + β2Rjt–1 + β3GVARjt + β4YVARjt + εjt DISPLAY Table Table 10Asjt = αj + γt + β1djt + β2Rjt–1 + εjt DISPLAY Table Table 10Bsjt = αj + γt + β1djt + β2Rjt–1 + β3GVARjt + β4YVARjt + εjt DISPLAY Table
All of the results serve as a strong repudiation of any type of optimizing behavior on the part of U.S. states over the time period studied. They do not take corrective actions in response to the accumulation of debt and thus do not satisfy an intertemporal budget constraint. This result contrasts with those of Bohn (  1998 1998), which finds that the U.S. federal government satisfies an intertemporal budget constraint, and Mendoza and Ostry (  2008 2008), which uses panels of advanced and emerging countries and finds that fiscal policy is responsible.
Why do results for the states differ from those for the U.S. federal government found in Bohn (  1998 1998)? One explanation is that the states believe that they will be helped either by other branches of state government, like the judicial branch, or by the federal government – where federal help need not be in the form of an explicit bailout. For example, during the time period of this study, states implemented various strategies to garner payments from the federal government via its program for assisting state hospitals that served a “disproportionate share” of uninsured people and those receiving Medicaid, a health insurance program for those with low incomes which had low reimbursement rates. In a study of disproportionate share payments, Ku and Coughlin (  1995 1995) concluded that the programs were usually created to generate extra revenue for the overall state budget: “How did the States use the additional $4.9 billion gained through these mechanisms? … the common reply was that ‘money is fungible’. The additional funds generally flowed into State general fund coffers, were mixed with other state funds…”.
Also during this time period, states were pursuing legal action against tobacco companies. Major cigarette producers entered into a Master Settlement Agree ment in 1998 with 46 states that had sued to recover health care costs related to treating smokers. In return for giving up future legal claims, the states received payments in perpetuity as compensation for smoking-related taxpayer-paid health care. The MSA did not require states to use their ongoing settlement payments for tobacco control programs. In 2007 the GAO (Shames,  2007 2007) found that from 2000-2005, while 30% of the payments went to health care, the next highest total, 22.9%, went to cover budget shortfalls (and the lowest share, 3.5%, went to tobacco-control programs).
An out-of-sample example that again illustrates the possibility of states’ abilities to access one-off funding occurred in 2011, when Google settled a Department of Justice suit by forfeiting $500 million for allowing Canadian pharmacies to illegally sell prescription drugs to U.S. consumers through Google’s AdWords program. The forfeited money was split between federal agencies, e.g. the FDA and IRS, and Rhode Island state and local law enforcement agencies (about $230 million) that helped in the investigation. How exactly did Rhode Island use its portion of the forfeiture?
“The settlement by Google, which was announced a year ago, has been used in part to relieve the underfunded pensions for retired policemen in two small Rhode Island cities, East Providence and North Providence. This unique deployment of $70 million (or 15% of the $500 million forfeiture) was made possible through the intervention of Rhode Island Senator Sheldon Whitehouse, who prevailed upon Attorney General Eric Holder to bypass restrictions on the rules for the use of such criminal proceeds. Sen. Whitehouse called this settlement “a transformational financial moment” in that the proceeds ordinarily could be used only for law enforcement investigations, training and equipment. Attorney General Holder acquiesced in allowing the money to be used to relieve some of the underfunded pension plans for retired policemen in Rhode Island (Lenzner,  2014 2014).
The examples discussed above suggest one reason for a finding of unsustainable fiscal behavior by states: they have some ability to engage strategically with the federal government with respect to obtaining funds. States may also be able to rely on one-off events not available at the federal/sovereign level where judicial settlements, for example, would be too small to have any significant budgetary impacts.
6 Conclusion
Using the empirical framework of Bohn ( 1998) and Barro ( 1998) and Barro ( 1986), which build on Barro’s ( 1986), which build on Barro’s ( 1979) tax smoothing model, this paper investigates the response of U.S. states’ primary surplus-income ratios to their debt-income ratios as a test of the sustainability of state fiscal policy. In contrast to the findings of Bohn ( 1979) tax smoothing model, this paper investigates the response of U.S. states’ primary surplus-income ratios to their debt-income ratios as a test of the sustainability of state fiscal policy. In contrast to the findings of Bohn ( 1998) that the U.S. federal government responds to increases in its debt-income ratios by increasing its primary surplus, results for a sample of U.S. states during the period 1978-1998 indicate no response to a rising debt-income ratio: that is, they were not fiscally “responsible”. Additionally, it is found that during this period U.S. states did not respond to credit market pressure, in the sense that the primary budget surplusincome ratio did not increase in response to an increasing risk premium. 1998) that the U.S. federal government responds to increases in its debt-income ratios by increasing its primary surplus, results for a sample of U.S. states during the period 1978-1998 indicate no response to a rising debt-income ratio: that is, they were not fiscally “responsible”. Additionally, it is found that during this period U.S. states did not respond to credit market pressure, in the sense that the primary budget surplusincome ratio did not increase in response to an increasing risk premium.
Funding
The author declares no financial or non-financial interests related to the research in this paper.
Notes
* The author thanks two anonymous referees for helpful comments.
* The author thanks two anonymous referees for helpful comments.
Disclosure statement
No potential conflict of interest was reported by the author.
References
Andersen, A. [et al.], 2014. The Impact of Late Budgets on State Government Borrowing Costs. Journal of Public Economics, 109(1), pp. 27-35 [ CrossRef]
Arellano, M. and Bond, S., 1991. Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations. Review of Economic Studies, 58(2), pp. 277-297 [ CrossRef]
Balassone, F. and Franco, D., 2000. Assessing Fiscal Sustainability: A Review of Methods with a View to EUM. Proceedings to the Bank of Italy Public Finance Workshop on Fiscal Sustainability, 21-60 [ CrossRef]
Barro, R., 1979. On the Determination of the Public Debt. Journal of Political Economy, 87(5), pp. 940-971 [ CrossRef]
Barro, R., 1986. U.S. Deficits since World War I. Scandinavian Journal of Economics, 88(1), pp. 195-222 [ CrossRef]
Barro, R., 1989. The Neoclassical Approach to Fiscal Policy. In: R. Barro, ed. Modern Business Cycle Theory. Cambridge: Harvard University Press.
Bayoumi, T., Goldstein, M. and Woglom, G., 1995. Do Credit Markets Discipline Sovereign Borrowers? Evidence from the U.S. States Journal of Money, Credit and Banking, 27(4), pp. 1046-59 [ CrossRef]
Bohn H., 1995. The Sustainability of Budget Deficits in a Stochastic Economy. Journal of Money, Credit and Banking, 27(1), pp. 257-271 [ CrossRef]
Bohn H., 2007. Are Stationarity and Cointegration Restrictions Really Necessary for the Intertemporal Budget Constraint? Journal of Monetary Economics, 54(7), pp. 1837-1847 [ CrossRef]
Bohn H., 2008. The Sustainability of Fiscal Policy in the United States In: R. Neck and J. E. Sturm, eds. Sustainability of Public Debt. Cambridge: MIT Press [ CrossRef]
Bohn, H. and Inman, R., 1996. Balanced Budget Rules and Public Deficits: Evidence from the U.S. States. Carnegie-Rochester Conference Series on Public Policy, 45(1), pp. 13-76 [ CrossRef]
Bohn, H., 1991. Budget Balance through Revenue or Spending Adjustments? Some Historical Evidence for the United States. Journal of Monetary Economics, 27(3), pp. 333-359 [ CrossRef]
Bohn, H., 1998. The Behavior of U.S. Public Debt and Deficits. Quarterly Journal of Economics, 113(3), pp. 949-63 [ CrossRef]
Chaney, B., Copley, P. and Stone, M., 2002. The effect of fiscal stress and balanced budget requirements on the funding and measurement of state pension obligations. Journal of Accounting and Public Policy, 21(4–5), pp. 287-313 [ CrossRef]
Goldstein, M. and Woglom, G., 1992. Market-based Fiscal Discipline in Monetary Unions: Evidence from the US Municipal Bond Market. In: M. Canzoneri, V. Grilli and P. Masson, eds. Establishing a Central Bank: Issues in Europe and Lessons from the US. New York: Cambridge University Press.
Greiner, A., Köller, U. and Semmler, W., 2007. Debt Sustainability in the European Monetary Union: Theory and Empirical Evidence for Selected Countries. Oxford Economic Papers, 59(2), pp. 194-218 [ CrossRef]
Hakkio, G. and Rush, M., 1991. Is the Budget Deficit ‘too large’? Economic Inquiry, 29(3), pp. 429-445 [ CrossRef]
Hamilton, J. and Flavin, M., 1986. On the Limitations of Government Borrowing: A Framework for Empirical Testing. American Economic Review, 76(4), pp. 808-819.
Holtz-Eakin, D., Rosen, H. and Tilly, S., 1994. Intertemporal Analysis of State and Local Government Spending: Theory and Tests. Journal of Urban Economics, 35(2), pp. 159-74 [ CrossRef]
Kremers, J., 1989. U.S. Federal Indebtedness and the Conduct of Fiscal Policy. Journal of Monetary Economics, 23(2), pp. 219-38 [ CrossRef]
Ku, L. and Coughlin, T., 1995. Medicaid Disproportionate Share and Other Special Financing Programs. Health Care Financing Review, 16(3), pp. 27-54.
Kula, M., 2014. Are U.S. State and Local Governments Consumption Smoothers? Journal of Economic Studies, 41(1), pp. 87-100 [ CrossRef]
Liu, P. and Thakor, A., 1984. Interest Yields, Credit Ratings, and Economic Characteristics of State Bonds: An Empirical Analysis. Journal of Money, Credit, and Banking, 16(3), pp. 345-351 [ CrossRef]
Mendoza, E.G. and Ostry, J. D., 2008. International Evidence on Fiscal Solvency: Is Fiscal Policy ‘Responsible’. Journal of Monetary Economics, 55(6), pp. 1081-1093 [ CrossRef]
Park, S., 1997. The Relationship between Government Financial Condition and Expected Tax Rates Reflected in Municipal Bond Yields. National Tax Journal, 50(1), pp. 23-38.
Poterba, J. and Rueben, K., 1999. State Fiscal Institutions and the U.S. Municipal Bond Market. In: J. Poterba and J. von Hagen, eds. Fiscal Institutions and Fiscal Performance. Chicago, IL: University of Chicago Press and NBER [ CrossRef]
Poterba, J. and Rueben, K., 2001. Fiscal News, State Budget Rules, and Tax- Exempt Bond Yields. Journal of Urban Economics, 50(3), pp. 537-562 [ CrossRef]
Quintos, C., 1995. Sustainability of the Deficit Process with Structural Shifts. Journal of Business and Economic Statistics, 13(4), pp. 409-417 [ CrossRef]
Sahasakul, C., 1986. The U.S. Evidence of Optimal Taxation Over Time. Journal of Monetary Economics, 18(3), 251-75 [ CrossRef]
Sørensen, B., Wu, L. and Yosha, O., 2001. Output Fluctuations and Fiscal Policy: US State and Local Governments 1978 – 1994. European Economic Review, 45(7), pp. 1271-1310 [ CrossRef]
Trehan, B. and Walsh, C., 1988. Common Trends, the Government Budget Constraint, and Revenue Smoothing. Journal of Economic Dynamics and Control, 12(2-3), pp. 425-44 [ CrossRef]
Trehan, B. and Walsh, C., 1991. Testing Intertemporal Budget Constraints: Theory and Applications to U.S. Federal Budget and Current Account Deficits. Journal of Money, Banking and Credit, 23(2), pp. 206-223 [ CrossRef]
Andersen, A. [et al.], 2014. The Impact of Late Budgets on State Government Borrowing Costs. Journal of Public Economics, 109(1), pp. 27-35 [ CrossRef]
Arellano, M. and Bond, S., 1991. Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations. Review of Economic Studies, 58(2), pp. 277-297 [ CrossRef]
Balassone, F. and Franco, D., 2000. Assessing Fiscal Sustainability: A Review of Methods with a View to EUM. Proceedings to the Bank of Italy Public Finance Workshop on Fiscal Sustainability, 21-60 [ CrossRef]
Barro, R., 1979. On the Determination of the Public Debt. Journal of Political Economy, 87(5), pp. 940-971 [ CrossRef]
Barro, R., 1986. U.S. Deficits since World War I. Scandinavian Journal of Economics, 88(1), pp. 195-222 [ CrossRef]
Barro, R., 1989. The Neoclassical Approach to Fiscal Policy. In: R. Barro, ed. Modern Business Cycle Theory. Cambridge: Harvard University Press.
Bayoumi, T., Goldstein, M. and Woglom, G., 1995. Do Credit Markets Discipline Sovereign Borrowers? Evidence from the U.S. States Journal of Money, Credit and Banking, 27(4), pp. 1046-59 [ CrossRef]
Bohn H., 1995. The Sustainability of Budget Deficits in a Stochastic Economy. Journal of Money, Credit and Banking, 27(1), pp. 257-271 [ CrossRef]
Bohn H., 2007. Are Stationarity and Cointegration Restrictions Really Necessary for the Intertemporal Budget Constraint? Journal of Monetary Economics, 54(7), pp. 1837-1847 [ CrossRef]
Bohn H., 2008. The Sustainability of Fiscal Policy in the United States In: R. Neck and J. E. Sturm, eds. Sustainability of Public Debt. Cambridge: MIT Press [ CrossRef]
Bohn, H. and Inman, R., 1996. Balanced Budget Rules and Public Deficits: Evidence from the U.S. States. Carnegie-Rochester Conference Series on Public Policy, 45(1), pp. 13-76 [ CrossRef]
Bohn, H., 1991. Budget Balance through Revenue or Spending Adjustments? Some Historical Evidence for the United States. Journal of Monetary Economics, 27(3), pp. 333-359 [ CrossRef]
Bohn, H., 1998. The Behavior of U.S. Public Debt and Deficits. Quarterly Journal of Economics, 113(3), pp. 949-63 [ CrossRef]
Chaney, B., Copley, P. and Stone, M., 2002. The effect of fiscal stress and balanced budget requirements on the funding and measurement of state pension obligations. Journal of Accounting and Public Policy, 21(4–5), pp. 287-313 [ CrossRef]
Goldstein, M. and Woglom, G., 1992. Market-based Fiscal Discipline in Monetary Unions: Evidence from the US Municipal Bond Market. In: M. Canzoneri, V. Grilli and P. Masson, eds. Establishing a Central Bank: Issues in Europe and Lessons from the US. New York: Cambridge University Press.
Greiner, A., Köller, U. and Semmler, W., 2007. Debt Sustainability in the European Monetary Union: Theory and Empirical Evidence for Selected Countries. Oxford Economic Papers, 59(2), pp. 194-218 [ CrossRef]
Hakkio, G. and Rush, M., 1991. Is the Budget Deficit ‘too large’? Economic Inquiry, 29(3), pp. 429-445 [ CrossRef]
Hamilton, J. and Flavin, M., 1986. On the Limitations of Government Borrowing: A Framework for Empirical Testing. American Economic Review, 76(4), pp. 808-819.
Holtz-Eakin, D., Rosen, H. and Tilly, S., 1994. Intertemporal Analysis of State and Local Government Spending: Theory and Tests. Journal of Urban Economics, 35(2), pp. 159-74 [ CrossRef]
Kremers, J., 1989. U.S. Federal Indebtedness and the Conduct of Fiscal Policy. Journal of Monetary Economics, 23(2), pp. 219-38 [ CrossRef]
Ku, L. and Coughlin, T., 1995. Medicaid Disproportionate Share and Other Special Financing Programs. Health Care Financing Review, 16(3), pp. 27-54.
Kula, M., 2014. Are U.S. State and Local Governments Consumption Smoothers? Journal of Economic Studies, 41(1), pp. 87-100 [ CrossRef]
Liu, P. and Thakor, A., 1984. Interest Yields, Credit Ratings, and Economic Characteristics of State Bonds: An Empirical Analysis. Journal of Money, Credit, and Banking, 16(3), pp. 345-351 [ CrossRef]
Mendoza, E.G. and Ostry, J. D., 2008. International Evidence on Fiscal Solvency: Is Fiscal Policy ‘Responsible’. Journal of Monetary Economics, 55(6), pp. 1081-1093 [ CrossRef]
Park, S., 1997. The Relationship between Government Financial Condition and Expected Tax Rates Reflected in Municipal Bond Yields. National Tax Journal, 50(1), pp. 23-38.
Poterba, J. and Rueben, K., 1999. State Fiscal Institutions and the U.S. Municipal Bond Market. In: J. Poterba and J. von Hagen, eds. Fiscal Institutions and Fiscal Performance. Chicago, IL: University of Chicago Press and NBER [ CrossRef]
Poterba, J. and Rueben, K., 2001. Fiscal News, State Budget Rules, and Tax- Exempt Bond Yields. Journal of Urban Economics, 50(3), pp. 537-562 [ CrossRef]
Quintos, C., 1995. Sustainability of the Deficit Process with Structural Shifts. Journal of Business and Economic Statistics, 13(4), pp. 409-417 [ CrossRef]
Sahasakul, C., 1986. The U.S. Evidence of Optimal Taxation Over Time. Journal of Monetary Economics, 18(3), 251-75 [ CrossRef]
Sørensen, B., Wu, L. and Yosha, O., 2001. Output Fluctuations and Fiscal Policy: US State and Local Governments 1978 – 1994. European Economic Review, 45(7), pp. 1271-1310 [ CrossRef]
Trehan, B. and Walsh, C., 1988. Common Trends, the Government Budget Constraint, and Revenue Smoothing. Journal of Economic Dynamics and Control, 12(2-3), pp. 425-44 [ CrossRef]
Trehan, B. and Walsh, C., 1991. Testing Intertemporal Budget Constraints: Theory and Applications to U.S. Federal Budget and Current Account Deficits. Journal of Money, Banking and Credit, 23(2), pp. 206-223 [ CrossRef]
|







 2000
2000