|
|
|
Abstract
This paper provides an overview of the evolution of private returns to schooling in the Portuguese economy along the 1986-2013 period. We estimate the returns separately for men and women, at the mean and along the conditional wage distribution. Returns to schooling are found to be high, particularly for women, and to increase along the distribution. The magnitude of the returns increased throughout the 1986-2013 period, but particularly in the 1990s. We also provide estimates of the relative wage premium associated with specific levels of educational attainment and find that they are highest for tertiary education. In the first decades under analysis, relative wage premia associated with the 9th grade stand above those estimated for secondary education, whereas in the most recent period these differences are negligible.
Keywords: returns to schooling; quantile regression; education
JEL: I26, J31, C21
1 Introduction
As formalized in Becker ( 1962), assessment of the private returns to schooling provides a key piece of information for an individual decision determining the optimal level of investment in formal education.
Regardless of the potential social returns to education, information on private returns is also relevant for policymakers, guiding them in the design of programs and incentive schemes to promote individual investment in education. There is a wide strand of empirical literature shedding light on the magnitudes and explanatory factors of returns to schooling in both advanced and emerging economies. Card ( 1999) provides a comprehensive review of existing literature on returns to schooling.
Cross-country estimates presented in Psacharopoulos ( 1994), Martins and Pereira ( 2004), Psacharopoulos and Patrinos ( 2004), and Montenegro and Patrinos ( 2014), show that returns to schooling in Portugal rank high among European Union countries. Vieira ( 1999), using data for the 1982-1992 period, found evidence of returns to schooling of approximately 7 per cent at the mean of the wage distribution. Acknowledging that conventional estimates based on Mincerian equations are hampered by the so-called “ability bias”, Vieira ( 1999) attempts to circumvent this by estimating the returns to schooling using instrumental variables (IV). Specifically, the author uses changes to compulsory schooling legislation as an exogenous source of variation in educational attainment. This results in lower – albeit still positive – returns to education. Sousa, Portela and Sá ( 2015) also focus only on returns at the mean of the distribution. Using Quadros de Pessoal data (QP henceforth) spanning the 1986-2009 period and a standard Mincer equation, they found returns of 10.0 per cent in the case of men and close to 10.5 per cent for women in the last year under analysis. Sousa, Portela and Sá ( 2015) also use IV, presenting results based on three different instruments: changes to compulsory education, quarter of birth and the average education by region in the year the individual first entered school. In this case estimates of returns to schooling are higher than those obtained using OLS, but show a similar evolution over time.
There are other studies that assess the returns at different points of the conditional wage distribution – not only at the mean. Machado and Mata ( 1998), using QP data for the 1982-1994 period, found returns ranging from 4 to 11 per cent, respectively, at the lower and upper parts of the distribution (and around 7-8 per cent at the mean). Similar evidence is provided in Hartog, Pereira and Vieira ( 2001). In the latter case, however, the authors consider a richer set of covariates in the regressions, which yields slightly lower returns than in Machado and Mata ( 1998). Martins and Pereira ( 2004) also provide estimates of returns to schooling at different points of the distribution. Using the 1995 wave of QP, they find increasing returns along the distribution (of 6.5 and 14.5 per cent, respectively, at the bottom and at the top of the distribution).
Alves, Venteno and Novo ( 2010), and Portugal ( 2004) provide estimates of the returns to tertiary education. In both cases, the authors find positive and significant returns benefiting individuals with university degrees (relative to non-university educated counterparts). Alves, Venteno and Novo ( 2010) provide estimates of the tertiary education wage premium at different points of the distribution and on the basis of QP data for 1982, 1995 and 2006. In the latter year they find returns ranging from approximately 45 per cent to almost 100 per cent, respectively, at the lower and upper quantiles of the distribution.
The recent evolution of returns to schooling in Portugal may however have changed, reflecting important reshufflings in the educational composition of the labor force that may have affected the way the market values education and specific schooling levels. This paper aims to complement the existing evidence on returns to schooling in the Portuguese economy and provide an overview of how they have changed since the late 1980s. In particular, we use QP data spanning the 1986-2013 period to estimate the returns to schooling separately for men and women, at the mean and along the conditional wage distribution. We also provide estimates of the relative wage premium associated with specific levels of educational attainment. The main goal of this paper is to provide a comprehensive description of the evolution of returns to schooling in this period, without claiming a causal relationship between schooling and earnings.
In broad terms, our results may be summarized as follows: the returns to schooling are found to be high, particularly in the case of women, and to increase along the distribution. The returns are highest for tertiary education. In the first decades under analysis, relative returns to the 9 th grade stand above those estimated for secondary education. In the most recent period these differences are negligible, in line with the typical evolution in advanced economies (Montenegro and Patrinos, 2014). The detailed analysis undertaken in this paper allows the pinpointing of exceptions to these general findings.
It is worth highlighting that we do not resort to IV or control function methods for estimating the private returns to schooling. Estimates based on these methods are highly dependent on the sub-sample whose schooling attainment is affected by the change in the instrument chosen for the analysis. Different instruments yield different estimates of the returns to schooling and lead to different interpretations (Imbens and Angrist, 1994). Moreover, we are interested in providing a broad picture of how returns have changed along the 1986-2013 period and, as shown in Sousa, Portela and Sá ( 2015), relying on IV estimates does not change the overall evolution. Finally, note also that our paper focuses only on the private (or individual) returns to education and does not address the social returns to education.
The paper is organized as follows: section 2 presents the data source, also providing a comprehensive analysis of descriptive statistics. Section 3 describes the theoretical framework underlying the estimations presented in the article, whereas section 4 sheds light on the strategy used to implement the analysis. Section 5 lists the key results of the article. Finally, section 6 presents the main conclusions and discusses topics relevant in terms of education policy.
2 Data description
Data are drawn from Quadros de Pessoal, a matched employer-employee dataset including a personal identification number that allows the tracing of individuals across time. The information is based on a compulsory survey conducted annually by the Ministry of Social Security. Data cover every establishment paying wages in the Portuguese private sector: general government, military staff, self-employed and household employees are thus excluded. The questionnaire covers attributes of workers and firms. Regarding the former, it includes information on gender, age, education, occupation, industry, tenure and earnings, among other dimensions. For the purpose of our analysis, we use data covering the 1986-2013 period (except 1990 and 2001, for which data are not available). We focus on a subsample made of full- and part-time employees aged between 16 and 65 years.
We define wages as the sum of every work-related category of income (including base salary, overtime pay, and other regular payments). Hourly wages are adjusted for both normal and supplementary working hours. Real wages are computed on the basis of each year’s Consumer Price Index (taking 1986 as the base-year). In QP, individual educational attainment corresponds to a categorical variable reporting the highest level completed. 1 An additional variable providing information on the minimum number of school years required to complete the highest educational level reported was also created.
Table 1 briefly describes selected QP waves used for the analysis. It provides evidence of a remarkable increase in the average length of schooling, from 5.6 to 9.9 years, respectively in 1986 and 2013. This is consistent with a significant drop in the share of employees reporting lower educational levels and a strong increase in the percentage with either secondary or tertiary education (figure 1).
This evolution was particularly noticeable in the case of female employees. They are, on average, more educated than men throughout the entire period under analysis and this disparity widened in the last decade. In particular, the percentage of female employees with a university degree increased from 2.3 per cent in the 1986 wave of QP to 22.0 per cent in 2013 (panel D of figure 1).
Table 1Descriptive statistics DISPLAY Table
Figure 1Employees by level of educational attainment (percentage) DISPLAY Figure
In spite of their better educational endowments, QP data show that, on average, women earn consistently lower wages than male employees over the whole period (figure 2). Nonetheless, although the two genders have experienced similar real wage increases in the first part of the 1986-2013 period, women’s earnings have been growing more sharply than men’s since 2000 (figure 3). As emphasized in Cardoso et al. ( 2016), this evolution may be explained by a composition effect stemming from the higher educational level of the women joining the labor market. Indeed, on average, wages for university-educated women, who represent an increasing share of our sample, grew more than wages of males with the same educational level (figure 4).
Figure 2Average real wage per hour (in euro) DISPLAY Figure
Figure 3Real wage growth (index 1986=1) DISPLAY Figure
Figure 4Real wage growth for workers with tertiary education (index 1986=1) DISPLAY Figure
Figure 5 depicts the average real wage by educational level along the 1986-2013 period. As expected, wages increase with education but differences between workers with tertiary education and their less educated counterparts are particularly significant. This differential widened up to 1995, remained relatively constant up to the mid-2000s and, more recently, it has been shrinking.
Focusing on workers with lower educational levels, figure 5 also points out that while in the late 1980s wages of individuals who did not complete the 9th grade were considerably below those of workers who did, this difference almost disappears in more recent QP waves. Conversely, whereas in the beginning of the period average real wages were similar among workers with 9th grade education and those who have completed secondary schooling, the gap between the two groups has been widening since the 1990s.
For both genders the distribution of wages has shifted to the right and become slightly less compressed than in the late 1980s (details depicted in appendix). This increase in wage inequality was particularly noticeable at the upper tail of the distribution, and only up to the mid-1990s, having remained stable since then. The wage distribution is more compressed in the case of less educated individuals.
Figure 5Average hourly wage by educational level DISPLAY Figure
The educational composition of individuals across the distribution changed considerably along the 1986-2013 period. While in 1986 the share of workers with tertiary (or even secondary) educational attainment with below-median wages was low, it increases when focusing on the 2013 wave of QP (figure 6). Although this may reflect a wide range of aspects and changes in the composition of private employment or in the productive structure of the economy, it can also be interpreted as a symptom of over-education (a phenomenon that warrants further analysis but which is out of the scope of this paper).
Figure 6Educational composition of the wage distribution DISPLAY Figure
3 Theoretical framework
Becker (1962) pioneered in applying utility theory to investment in education. In his framework the proportional pecuniary returns associated with educational attainment are a key component of the individual decision on whether and by how much to invest in human capital. In particular, individuals select the optimal number of years of schooling so as to maximise the discounted present value of future earnings net of the cost of schooling. This corresponds to an optimization problem whose solution is such that individuals would continue to invest in additional education up to the point where marginal benefits match marginal costs. Mincer ( 1974) provided an empirical approximation to the marginal benefits’ side of the individuals’ optimization problem. In particular, the so-called traditional Mincerian wage equation corresponds to:
| lnyi = α + βSi + λ1Expi + λ2Exp2i + εi |
(1 ) |
where β corresponds to the pecuniary return from an additional year of formal education and Exp refers to individuals’ experience in the labor market. Like most writers on the relationship between education and earnings, we rely on Mincer’s framework for the estimation of the returns to schooling.
Card ( 1999) made it clear that the decision on how much to invest in schooling is very much conditional on individual preferences and that it is subject to individual heterogeneity, both in terms of the marginal returns to schooling (determined by, for instance, differences in individual ability) and in terms of its costs (accounting for differences in rates of substitution between schooling and future earnings on the basis of, e.g., access to funds or personal taste). This implies a heterogeneous effects framework in which the way covariates affect wages varies across individuals.
4 Empirical strategy
To estimate the returns to schooling in the Portuguese economy we adopt the standard approach relying on Mincerian wage regressions such as the one in equation (1). The regressions are run separately for each wave of QP, assuming a crosssectional set-up. We adopt a homogeneous effect framework, in the sense that we assume that the impact of schooling on wages is the same for all individuals: βi = β1 = ... = βN, for all i = 1,...,N.
Since our dataset does not include information on individuals’ labor market experience, we take age (as a second order polynomial) as a proxy. It should be noted that this is not an accurate measure because it fails to take into account, for instance, the years spent at school or university or in unemployment, yielding an overestimation of the amount of labor market experience. Our regressions include a set of other covariates: the individual’s tenure in the current firm (also as a second order polynomial), the logarithm of the current firm’s size and, when pooling dana jointly for men and women, gender dummies (equal to one for male employees). We allow for additional flexibility by running the wage regressions separately for men and women using the same set of covariates, except for the gender dummy. 2
It should be noted that, as pointed out by Card ( 2001), estimates of returns to schooling based on Mincerian wage equations may be hampered by sources of bias. In the first place, there may be mismeasurements in terms of the individual schooling, in which case estimates of β would be downward biased. Although the possibility of measurement errors cannot be ruled-out, as we are using an administrative dana source we are confident that erroneous cases are negligible in our sample.
An additional source of bias arises from the fact that we are not controlling for the whole set of individual-specific attributes that affect wages (“ability bias”). These factors – some of which are not observable – are included in error term. If they are also correlated with schooling attainment, generating endogeneity, the estimator would also be inconsistent. Since the standard Mincerian equation does not account for the impact of individual innate ability (or other unobservables) on wages and educational level, β̂ would be upward biased. There are several possible solutions to circumvent these issues, based on finding appropriate proxies for the unobserved factors or by applying specific econometric methods (such as IV or control function).
However, in this paper we do not resort to these solutions because no suitable proxy variables are available in the dataset and estimates based on the aforementioned methods would be highly dependent on the subsample whose schooling attainment is affected by the change in the elected instruments (Imbens and Angrist, 1994). Moreover, we are interested in providing a broad overview of returns to schooling along the 1986-2013 period and not on analyzing causal relationships; since the unobserved factors that may be biasing our results are unlikely to change over time, they do not affect the evolution of the returns – only their magnitude. This is confirmed by results presented in Sousa, Portela and Sá ( 2015), which show that controlling for endogeneity does not change the way the returns evolved over time.
Finally, one should bear in mind that estimates of returns to education based on Mincerian regressions do not take into account the effect of costs and taxes that individuals incur by investing in education. Therefore, as thoroughly discussed in Heckman, Lochner and Todd ( 2006), Mincer-based returns such as those we present in this paper fail to provide an accurate depiction of the actual internal rate of return to schooling and shall not be interpreted as such.
4.1 Returns to an additional year of schooling
Our baseline specification corresponds to
| lnyi = α + βSi + λ1agei + λ2age2i + xiTγ + εi |
(2) |
where yi corresponds to individuals’ real hourly wage and Si represents the minimum number of schooling years required to complete the highest level reported by the individual. As such, coefficient β, our parameter of interest, represents the per cent increase in hourly wage resulting from an additional year of schooling estimated using Ordinary Least Squares (OLS). Vector xi groups the set of observable characteristics aforementioned and estimates for the parameters in vector γ measure the respective marginal impact on yi.
Finally, the marginal impact of age is given by λˆ1 + 2 * λˆ2agei, where agei refers to the worker’s age.
In spite of adopting a homogeneous effect set-up, we allow for some heterogeneity in the returns by letting them change depending on the individuals’ placement along the conditional distribution of wages. In particular, we also run our baseline specification within the Quantile Regression (QR) framework proposed in Koenker and Bassett ( 1978). This allows our covariates to affect the shape and tail behavior of the conditional wage distribution and implies assuming | lnyi = αθ + βθSi + λ1,θ agei + λ2,θ agei2 + xTi γθ + εθ,i, | (3) |
where θ represents different quantiles of the conditional distribution of hourlywages: θ = {0.1,0.25,0.5,0.75,0.9}. Therefore, βθ corresponds to the return to an additional year of schooling at the θ-th quantile of distribution of the logarithm of hourly wages conditional on the individuals’ observed attributes. By assessing the returns to schooling at these different quantiles, we complement the evidence provided y OLS, which refers to the mean of the wage distribution.
4.2 Returns to specific education levels
In addition to the baseline specification, we also consider an alternative specification in which the highest completed level of schooling is included on the basis of dummy variables: 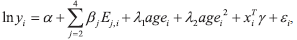 | (4) |
where Ej, j = {1,2,3,4}, are indicator variables that equal one for individuals reporting each of the following levels of schooling attainment: (1) less than the 9th
grade; (2) 9th grade; (3) secondary education; and (4) tertiary education. The first category is omitted in the regressions. In this case each βj, j >1 corresponds to the wage premium benefiting individuals holding schooling level j vis-à-vis comparable counterparts with less than the 9th grade (j =1). We also implement this alternative specification within a QR framework:
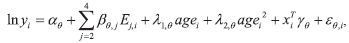 | (5) |
5 Findings
5.1 Returns to an additional year of schooling
Figure 7 presents the estimates of returns to schooling obtained from OLS regressions with specification (2) in each available wave of QP. Table 2 presents the full set of results of non-gender-specific regressions for selected years, including the results of the estimation of specification (2) controlling for industry and region effects. The introduction of these additional covariates does yield a decrease in the magnitude of the returns to schooling, but the overall picture does not change.
Figure 7OLS-based returns to an additional year of schooling DISPLAY Figure
The results provide evidence of positive returns to an additional year of schooling in the case of both men and women. In the latter, the estimated returns are slightly higher, over the whole period under analysis: in 2013, an additional year of schooling is estimated to yield, on average, a 7.6 per cent increase in females’ hourly wage, whereas for men the estimated increment stands at 6.4 per cent. The gender gap in the returns is statistically significant along the entire period and has remained relatively stable since 1986. Over time, there has been a slight increase in the returns for both genders. This was particularly marked along the 1990s and in more recent decades the returns remained relatively constant, albeit with a minor drop as of 2009. 3
Results presented in figure 7 refer to the estimates of returns to an additional year of schooling at the mean of the conditional wage distribution. Such evidence may hide important differences at different points of the distribution. By relying on the QR framework we are able to estimate the returns to schooling at different quantiles. Results obtained with this methodology are summarized in figure 8 and table 3.
Figure 8Returns to schooling across the wage distribution (per cent) DISPLAY Figure
These results indeed show that the magnitude of the estimates for the returns to schooling changes considerably along the distribution. For instance, estimates obtained on the basis of OLS using the 2013 wave of QP and pooling data for both men and women point that an additional year of schooling implies a mean 7.1 per cent increase on wages (table 2). This figure masks the fact that, applying the same procedure to the same data but using the QR framework, one additional year of schooling yields a 3.1 per cent wage increase at the 1st decile of the distribution and an 8.8 per cent impact at the 9th (table 3).
Table 2Wage regressions – OLS DISPLAY Table
In fact, estimates of returns to schooling increase along the wage distribution. This feature holds for both genders, but it is particularly noticeable in the case of women. Evidence presented in figure 8 also makes it clear that the increase in returns to schooling along 1986-2013 period holds only for individuals placed above the 25 th quantile of the wage distribution. Returns estimated at its lower tail using the 2013 QP wave stand below those obtained using the 1986 data. Moreover, up to 2003, evidence of higher returns for women also holds only above the 1 st decile of the distribution. 4
The comparison between returns to schooling estimated at different points of the distribution provides a measure of their dispersion. Such a comparison, illustrated in figure 9, shows in the first place that, across the whole distribution, returns are more dispersed among women than among men. In both cases, inequality in returns widened along the 1986-2013 period, but it was particularly noticeable in the case of female employees and in the early 1990s. This evolution seems to be largely driven by developments at the lower part of the conditional wage distribution, since at the upper quantiles inequality in returns has remained relatively stable. Moreover, among high earners variability in the returns is lower than at the lower part of the wage distribution.
Figure 9Dispersion in returns to schooling (percentage points) DISPLAY Figure
5.2 Returns to specific education levels
On the basis of specifications (4) and (5) it is possible to assess the average wage premium associated with specific levels of education. In this case, coefficients βj, j = {2,3,4}, represent the wage gain from completing schooling level j relative to individuals who have not completed the 9th grade (corresponding to education level j =1, the omitted category). Table 4 provides detailed results for selected years.
Table 3Wage regressions – Quantile regressions DISPLAY Table
As we are interested in the wage gain relative to the schooling level immediately before, we plot in figure 10 the difference in the coefficients estimated using specification (4) as follows:
In the first place, figure 10 confirms that women benefit from larger returns to education than men, except as regards the relative premium associated with tertiary education in the first years of the sample. It also shows that the increase over time in overall returns to schooling documented in the previous subsection is largely driven by the evolution of the premium associated with tertiary education. Indeed, in the beginning of the 1986-2013 period, completing a university degree is estimated to yield male workers a 34.3 per cent premium vis-à-vis completing secondary education, while for women such figure stands at 33.1 per cent. Results obtained using the 2013 wave of QP imply that men holding a university degree enjoy a 44.9 per cent wage premium relative to comparable workers who complete only secondary education. For women, the comparable figure stands at 49.6 per cent.
Figure 10Returns to schooling at the mean of the wage distribution by educational attainment (per cent) DISPLAY Figure
Regarding secondary education, there is evidence that the gain relative to completing only the 9th grade increased along the 1986-2013 period, but it is still considerably below that referring to tertiary education: 16.8 per cent for men and 20.4 per cent for women. The increase in the premia estimated for secondary and tertiary education occurred against a background of an expansion in the pool of workers holding these schooling levels, suggesting that it may have been demanddriven.
Table 4Wage regressions – OLS DISPLAY Table
The premium for tertiary education increased markedly in the first half of the 1990s – especially in the case of women – and then remained stable up to 2009, when there is a minor decline in its magnitude. Evidence from regressions focusing specifically on university-educated individuals aged between 25 and 45 suggests that the younger workers benefit from lower returns to schooling and have experienced a slightly larger drop in returns than the overall sample (figure 11).
Finally, it is worth highlighting the sharp decline in the premium associated with completing the 9 th grade. In the late 1980s, it was very close to the relative wage gain enjoyed by individuals holding a university degree (in the case of women it was in fact higher). Since then, our estimates suggest a decline and the magnitude estimated on the basis of 2013 data corresponds to approximately half the figure obtained with the 1986 QP wave. This evolution is in line with the pattern typically found for advanced economies (Montenegro and Patrinos, 2014).
The drop in returns to the 9th grade has been accompanied by an increase in the share of employees reporting it as the highest level completed (and a sharp decline in those holding less than the 9th grade). This evolution, plotted in figure 12, may be related to the fact that compulsory schooling was extended to the 9th grade in 1986. The measure applied only to individuals born as of 1980, which would be showing up in QP data as of 1996.
Figure 11Returns to tertiary education in the post-2009 period for younger cohorts (per cent) DISPLAY Figure Figure 12Returns to completing the 9th grade vs share of individuals with the 9th grade DISPLAY Figure Figure 13Returns to schooling across the wage distribution by educational attainment (per cent) DISPLAY Figure Table 5Wage regressions – Quantile Regressions DISPLAY Table
However, even older individuals who were still attending school in 1986 may have anticipated that the market would start valuing completion of the 9th grade and decided to study longer – either to complete just the 9th grade or further levels to obtain a differentiation factor. This would result in a decline in the share of individuals with less than the 9th grade even before the first cohorts affected by the legal change joined the labor force. Although it is not possible to establish a causal link between this decline and the drop in returns to the 9th grade, ceteris paribus, an expansion in the pool of workers who have completed the latter level would in principle result in such an evolution. This suggests that the drop in the premium for completing the 9th grade was supply-driven. Additionally, this evolution may have been reinforced by selection effects. In particular, it is arguable that the individuals who drop out after completing the 9th grade in the recent period differ from those who did it some years or decades ago, in terms of characteristics that may result in lower returns to schooling (for example, younger 9th grade drop-outs may be expected to have, on average, poorer innate ability endowments, or less favorable family backgrounds).
Evidence obtained from QR estimates of specification (5), presented in figure 13 and in greater detail in table 5, shows that, for women, the relative premium from completing tertiary education increases along the wage distribution. In the case of male employees, such evidence holds only below the 9th decile. Figure 13 also suggests that the rise in the relative return to university degrees occurred throughout the wage distribution, but it is more noticeable at the upper quantiles and in the case of women. Regarding the already mentioned drop in the magnitude of returns as of 2009, it appears to result from developments at the lower tail of the conditional distribution. Finally, regarding the premia estimated for completing secondary education and the 9th grade, their average evolutions are driven by results in the upper quantiles, as below the median of the wage distribution they have remained broadly constant.
6 Discussion and concluding remarks
Portuguese economy. The returns increased in the late 1980s and the 1990s, especially as regards tertiary education. This occurred in parallel with an expansion of the pool of workers holding university degrees, suggesting it was surpassed by a rise in the demand for skilled labor. During the late 1990s and early 2000s, returns remained relatively constant, largely reflecting the stabilization of the wage premium for tertiary education. In the post-2009 period, however, our results point to a minor decrease in the magnitude of the returns, in the case of both tertiary and secondary education.
In spite of these changes along the 1986-2013 period, the overall picture does not change: the returns to schooling are found to be higher in the case of women and to increase along the wage distribution and with educational attainment: formal education appears to be more valued for women and highly paid and highly skilled jobs. Several factors may be put forward as possible explanations for the evolution of returns to schooling just described.
The phenomenon of over-education could be one of the drivers: over-education, measured as a non-negligible share of highly-educated workers in blue-collar occupations, results in their placement in the bottom quantiles of the wage distribution. This translates into low returns to schooling for these individuals and increases dispersion within the same educational level, thus contributing to explain the pattern of increasing returns along the distribution.
The effects of over-education may be a reflection of qualitative aspects of schooling: while the estimation of returns only takes into account the quantity of educational attainment, it disregards factors such as school quality or the different valuation attributed to different areas of study. Attending poor quality schools or investing in a field of study that receives low valuation in the labor market would, in principle, result in low-paid jobs and in positions requiring low skills.
We cannot rule out the possibility that the developments described are affected by the fact that individual differences in ability (or other unobserved attributes) are not being controlled for. In particular, it is expectable that differences in individual ability play a bigger role in explaining the dispersion in returns among more skilled workers. For low educated individuals, by contrast, the differences should be relatively smaller. Not controlling for these differences would result in an overestimation of returns to schooling in the upper quantiles of the distribution and reinforce the effects of over-education and low school quality.
In spite of focusing only on the private returns to education, our results unveil important messages for individuals and policymakers alike: in Portugal, education remains a profitable investment for individual agents and policymakers must take this into account when designing policies and incentive schemes.
The returns are highest for tertiary education and it is likely that individuals will continue to invest in education and, in particular, in university degrees. Compulsory schooling has recently been extended to 12 years, encompassing secondary education. This may also provide incentives for individuals that would otherwise leave school to go further and complete a tertiary educational level to differentiate themselves from the holders of secondary schooling. These factors would in principle result in the expansion of the student population in the next decades but are likely to be counteracted by demographic trends. Against a background of tight budgetary constraints, the challenge for policymakers is to ensure the quality of the public school system while providing low-income households the conditions to access tertiary level education. Moreover, this cannot be done at the expense of low quality preschool or elementary education, as investments in lower schooling levels increase the returns to subsequent ones 5. These tensions may require a reshuffling in terms of the funding sources of public expenditure on education policy. A common suggestion is to increase the share of costs supported by the individuals in tertiary education. This line of reasoning is based on the idea that social returns to schooling are relatively lower for tertiary levels, whereas private returns are high – a piece of evidence supported by our empirical findings. Examples of measures aimed at increasing individual participation in financing include mere increases in tuition or the recently higher education reform in the UK encompassing the setting-up of a loan scheme that is contingent on graduates’ future earnings. Resorting to this sort of measures may create additional leeway to reinforce support to low-income households.
Appendix
Details on the empirical distribution of the logarithm of hourly wages
Figure A1Distribution of real wages in 1986 and 2013 DISPLAY Figure
Figure A2Real wage dispersion DISPLAY Figure
Figure A3Real wage dispersion by educational attainment DISPLAY Figure
Notes
* We thank comments by Nuno Alves, Cláudia Braz, Isabel H. Correia, Andy Garin, Miguel Gouveia, Pedro Portugal, Pedro Raposo and participants in a seminar held at Banco de Portugal. Suggestions by two anonymous referees are also gratefully acknowledged. The views herein expressed are our own and do not necessarily coincide with those of Banco de Portugal or the Eurosystem.
1 More precisely, we consider the mode of the highest level of education reported throughout the panel. The difference between the mode and the actual level reported is negligible and does not change either the magnitude of the estimates or their evolution over time.
2 For the purpose of assessing robustness of the estimates, we also ran regressions including controls for industry and region. This brings down the magnitude of the coefficients associated with educational attainment, but the evolution of returns over time is unchanged.
3 Significance tests show that this drop, although small, is statistically significant.
4 Note that the differences in returns estimated on the basis of QR for the 1986 and 2013 waves of QP are found to be statistically significant.
5 Refer to Heckman and Cunha (2007).
* We thank comments by Nuno Alves, Cláudia Braz, Isabel H. Correia, Andy Garin, Miguel Gouveia, Pedro Portugal, Pedro Raposo and participants in a seminar held at Banco de Portugal. Suggestions by two anonymous referees are also gratefully acknowledged. The views herein expressed are our own and do not necessarily coincide with those of Banco de Portugal or the Eurosystem.
1 More precisely, we consider the mode of the highest level of education reported throughout the panel. The difference between the mode and the actual level reported is negligible and does not change either the magnitude of the estimates or their evolution over time.
2 For the purpose of assessing robustness of the estimates, we also ran regressions including controls for industry and region. This brings down the magnitude of the coefficients associated with educational attainment, but the evolution of returns over time is unchanged.
3 Significance tests show that this drop, although small, is statistically significant.
4 Note that the differences in returns estimated on the basis of QR for the 1986 and 2013 waves of QP are found to be statistically significant.
5 Refer to Heckman and Cunha ( 2007).
Disclosure statement
No potential conflict of interest was reported by the authors.
References
Becker, G. S., 1962. Investment in Human Capital: A Theoretical Analysis. Journal of Political Economy, 70(1), pp. 1–9.
Card, D., 1999. The causal effect of education on earnings in: O. Ashenfelter and D. Card, eds. Handbook of Labor Economics, Vol. 3 of Handbook of Labor Economics, pp. 1801–1863 [ CrossRef]
Card, D., 2001. Estimating the Return to Schooling: Progress on Some Persistent Econometric Problems. Econometrica, 69(5), pp. 1127-1160 [ CrossRef]
Hartog, J., Pereira, P. and Vieira, J., 2001. Changing returns to education in Portugal during the 1980s and early 1990s: OLS and quantile regression estimators. Applied Economics, 33(8), pp. 1021–1037 [ CrossRef]
Heckman, J. and Cunha, F., 2007. The Technology of Skill Formation. American Economic Review, 97(2), pp. 31–47 [ CrossRef]
Heckman, J., Lochner, L. J. and Todd, P. E., 2006. Earnings Functions, Rates of Return and Treatment Effects: The Mincer Equation and Beyond. Vol. 1 of Handbook of the Economics of Education, pp. 307–458 [ CrossRef]
Imbens, G. and Angrist, J., 1994. Identification and estimation of local average treatment effects. Econometrica, 62(2), pp. 467–75 [ CrossRef]
Koenker, R. W. and Bassett, G., 1978. Regression quantiles. Econometrica, 46(1), pp. 33–50 [ CrossRef]
Martins, P. S. and Pereira, P. T., 2004. Does education reduce wage inequality? Quantile regression evidence from 16 countries. Labour Economics, 11(3), pp. 355–371 [ CrossRef]
Mincer, J. A., 1974. Schooling, Experience, and Earnings. Washington: National Bureau of Economic Research, Inc.
Montenegro, C. E. and Patrinos, H. A., 2014. Comparable estimates of returns to schooling around the world. Policy Research Working Paper Series, No. 7020.
Portugal, P., 2004. Myths and Facts Regarding the Portuguese Labour Market - the Tragic Fate of College Graduates. Banco de Portugal Economic Bulletin, pp. 69-76.
Psacharopoulos, G. and Patrinos, H. A., 2004. Returns to investment in education: a further update. Education Economics, 12(2), pp. 111–134 [ CrossRef]
Psacharopoulos, G., 1994. Returns to investment in education: A global update. World Development, 22(9), pp. 1325–1343 [ CrossRef]
Vieira, J., 1999. Returns to education in Portugal. Labour Economics, 6(4), pp. 535– 541 [ CrossRef]
Becker, G. S., 1962. Investment in Human Capital: A Theoretical Analysis. J ournal of Political Economy, 70(1), pp. 1–9.
Card, D., 1999. The causal effect of education on earnings in: O. Ashenfelter and D. Card, eds. Handbook of Labor Economics, Vol. 3 of Handbook of Labor Economics, pp. 1801–1863 [ CrossRef]
Card, D., 2001. Estimating the Return to Schooling: Progress on Some Persistent Econometric Problems. Econometrica, 69(5), pp. 1127-1160 [ CrossRef]
Hartog, J., Pereira, P. and Vieira, J., 2001. Changing returns to education in Portugal during the 1980s and early 1990s: OLS and quantile regression estimators. Applied Economics, 33(8), pp. 1021–1037 [ CrossRef]
Heckman, J. and Cunha, F., 2007. The Technology of Skill Formation. American Economic Review, 97(2), pp. 31–47 [ CrossRef]
Heckman, J., Lochner, L. J. and Todd, P. E., 2006. Earnings Functions, Rates of Return and Treatment Effects: The Mincer Equation and Beyond. Vol. 1 of Handbook of the Economics of Education, pp. 307–458 [ CrossRef]
Imbens, G. and Angrist, J., 1994. Identification and estimation of local average treatment effects. Econometrica, 62(2), pp. 467–75 [ CrossRef]
Koenker, R. W. and Bassett, G., 1978. Regression quantiles. Econometrica, 46(1), pp. 33–50 [ CrossRef]
Martins, P. S. and Pereira, P. T., 2004. Does education reduce wage inequality? Quantile regression evidence from 16 countries. Labour Economics, 11(3), pp. 355–371 [ CrossRef]
Mincer, J. A., 1974. Schooling, Experience, and Earnings. Washington: National Bureau of Economic Research, Inc.
Montenegro, C. E. and Patrinos, H. A., 2014. Comparable estimates of returns to schooling around the world. Policy Research Working Paper Series, No. 7020.
Portugal, P., 2004. Myths and Facts Regarding the Portuguese Labour Market - the Tragic Fate of College Graduates. Banco de Portugal Economic Bulletin, pp. 69-76.
Psacharopoulos, G. and Patrinos, H. A., 2004. Returns to investment in education: a further update. Education Economics, 12(2), pp. 111–134 [ CrossRef]
Psacharopoulos, G., 1994. Returns to investment in education: A global update. World Development, 22(9), pp. 1325–1343 [ CrossRef]
Vieira, J., 1999. Returns to education in Portugal. Labour Economics, 6(4), pp. 535– 541 [ CrossRef]
|
